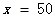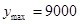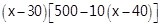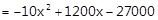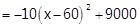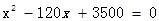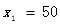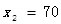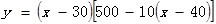最新亚洲精品,国产suv精品一区二区三区,综合在线影院

智能回答

某商品的進價為每件30元，現(xiàn)在的標價為每件40元，每星期可賣出150件。市場調查反映：如果每件的標價每漲1元

展開

沒找到滿意答案？去問豆包AI智能助手

取消復制問題

m18627004355

（1）求y和x的函數關系式還有x的范圍。
y = 150 - 10x，
銷量要滿足40 + x ≤ 45，所以x ≤ 5，
那x的取值范圍就是0 ≤ x ≤ 5。
（2）定價多少才能讓每星期利潤最大，而且銷量也大？最大利潤是多少？
設利潤W = (售價 - 成本價) × 銷量 = (40 - 30 + x) × y = (10 + x)(150 - 10x)
展開后：
W = -10x? + 50x + 1500
配方一下變成：
W = -10(x - 2.5)? + 1562.5
所以漲價2.5元時利潤最大，定價40 + 2.5 = 42.5元，
這時候銷量是150 - 10×2.5 = 125件，
最大利潤是1562.5元。
dajiba520000

（1）

.（2）當x=60時，

．

試題分析：（1）設售價定為x元時，每件賺取利潤為（x-30）元，每天買出【500-10（x-40）】件，每天賺取利潤

等于8000元,列方程即可. （2）設最大利潤為y元，由題可得:y=

由二次函數的性質可得結論.
試題解析：(1)解：設售價定為x元時，每天賺取利潤8000元，
由已知得：

整理得：

解得：

或

盡量減少庫存，

答：售價定為50元時，每天賺取利潤8000元。
（2）解：設最大利潤為y元，由題可得：

．

當x=60時，

．
a3619527

解：設應該降低x元
(60-x-30)(400+10x)=6000
(30-x)(400+10x)=6000
(30-x)(40+x)=600
(x-30)(x+40)+600=0
x?+10x-600=0
(x+30)(x-20)=0
x= -30（舍去）
x= 20
60-x=40
答：應定為40元/件，這時每月應進貨600件。

希望幫助到你，若有疑問，可以追問~~~
祝你學習進步，更上一層樓！(*^__^*)
dengzhihao1992

獲利是指：（售價-進價）/進價*100%
利潤=(300+20x)(60-x-40)=20(15+x)(20-x) x>0 降價
(300-10x)(60+x-40)=10(30-x)(20+x) x>0 漲價
figopei

設利潤為y，價格為x。則當x>60，即漲價時，y=【300-（冤剛尖赫獬雇鹼痰漿勘x-60）*10】*（x-40）=-10x*x+1300x-36000 當x<60，即降價時，y=【（60-x）*18+300】*（x-40）=-18x*x+2100x-55200 他們的圖像都是頂點向上的拋物線，所以當x=-b/2a時，y取得最大值。即當x=1300/2*10=65時，利潤y=6250元當x=2100/2*18=50時，利潤y=4800元，明顯，當定價x=65時，利潤取得最大值為6250元，為所求。
dsajbgznqyik

.y=300+18x(0<=x<=15)
2.由題目可知每星期的利潤是（20-x）*y（每件利潤*件數）
又因為y=300+18x,所以
利潤=（20-x）*（300+18x）
利潤=6000+360x-300x-18x2(2次方）
利潤=-18*(x2-(60/18)x+(900/324)+6000+50
利潤=-18*(x-(30/18))2+6050
當x=5/3時,利潤最大為6050
定價為175/3時，利潤最大為6050

第二題：因為有兩個不等實數根，△=（2（m-1)）2-4*（m2-3)>0
=4*(m2-2m+1)-4*(m2-3)>0
所以-2m-2>0
m<-1
penelope12345

解：（1）①y=90-x（30≤x≤40）

②y=130-2x（40（2）w①=（x-20）（90-x）=1000 解得：x[1]=40，x[2]=70（舍去） w②=（x-20）（130-2x）=1000 解得：x[1]=45，x[2]=40（舍去） ∴每件商品的售價定為40元或45元時，每周可獲利1000元