(1)利用三角恒等式,可知 $ tan C = sqrt{3} $,所以角 $ C = 60^circ $。
-
由題意及條件可得:
(1)利用三角恒等式,可知 $ tan C = sqrt{3} $,所以角 $ C = 60^circ $。 -
1)m∥n, ∴b/(2a-c)=cosb/cosc 正弦定理:a/sina=b/sinb=c/sinc ∴b/(2a-c)=sinb/(2sina-sinc)=cosb/cosc ∴2sinacosb=sinccosb sinbcosc=sin(b c)=sin(180°-a)=sina ∴cosb=1/2, b=60° 2)c=120°-a y=cos?a cos?c=(1 cos2a)/2 (1 cos2c)/2=1 (1/2)[cos2a cos2(120°-a)] =1 (1/2)[cos2a cos(240°-2a)]=1 (1/2)[cos2a-(1/2)cos2a-(√3/2)sin2a] =1 (1/2)[(1/2)cos2a-(√3/2)sin2a]=1 (1/2)cos(2a 60°) ∵0°<120°, ∴60°<2a 60°<300°, -1<=sin(2a 60°)<1/2 ∴1/2<=y<5/4, 即y取值范圍為[1/2,5/4)
-
-
a=1,A=60 b/sinB=c/sinC=a/sinA=2/√3 b+c=2/√3(sinB+sinC) B=(B+C)/2+(B-C)/2 C=(B+C)/2-(B-C)/2 sinB+sinC=sin[(B+C)/2]cos[(B-C)/2]+cos[(B+C)/2]sin[(B-C)/2]+sin[(B+C)/2]cos[(B-C)/2]-cos[(B+C)/2]sin[(B-C)/2] =2sin[(B+C)/2]cos[(B-C)/2] B+C=180-A=120 所以sinB+sinC=√3cos[(B-C)/2] B+C=120 B=120-C>0,0<120 所以B-C=2C-120 所以-120<120 -60<(B-C)/2<60 所以1/2
-
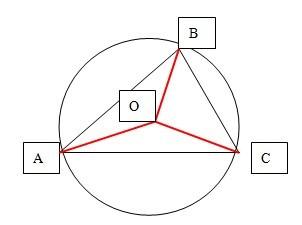
如圖,角B(即ABC)=60度,OA=OB=OC=r=1
角AOC=2角ABC(圓心角等于同弧上的圓周角的2倍)=120度
在三角形OAC中,AC^2=b^2=OA^2+OC^2-2OA*OC*cosAOC [^2指平方]
=1+1-2*1*1*cos120度=2-2*1*1*(-1/2)=3…………(1)
在三角形ABC中,b^2=a^2+c^2-2ac*cosABC=a^2+c^2-ac
于是a^2+c^2=b^2+ac…………(2)
另,根據(jù)正弦定理,a=bsinA/sinB c=bsinC/sinB
于是ac=b^2*sinAsinC/(sin^2 B)=b^2*sinAsinC/(3/4)=(4/3)*b^2*sinAsinC
=4/3*b^2*{-1/2*[cos(A+C)-cos(A-C)]} [積化和差]
= -2/3*b^2*[cos(180-B)-cos(A-C)]
= -2/3*b^2*[-cosB-cos(A-C)]
=2/3*b^2*[cosB+cos(A-C)]
=2/3*b^2*[1/2+cos(A-C)
=(b^2)/3+(2/3)*b^2*cos(A-C)………………(3)
把(1)和(3)代入(2)得
a^2+c^2=3+3/3+(2/3)*3cos(A-C)
=4+2cos(A-C)
下面分析其最大值:余弦的最大值為1,于是當(dāng)A-C=0時(shí),cos0=1,
a^2+c^2有最大值6,此時(shí),A=C=60度=B,是正三角形。
然后看最小值:余弦的最小值為0,于是當(dāng)A-C-90度時(shí),cos90度=0
a^2+c^2有最小值4,此時(shí),可算出A=105度,C=15度。
于是a^2+c^2的取值范圍是:4<a^2+c^2<6
-
√3cos(A+B)/2=√3cos(90-C/2)=√3sin(C/2)=sinC=2sin(C/2)cos(C/2) 所以cos(C/2)=√3/2,C=60 余弦定理:2ab*cosC=a2+b2-c2=ab。。。。1式 S=1/2ab*cosC=ab/4 a+b+c=12。。。。。。2式 由1,2式得:ab-8a-8b+48=0,而a+b>=2√ab,所以有ab-16√ab+48>=0,解得ab>=144(舍,太大了)或ab<=16, 所以S=ab/4<=4,最大為4,當(dāng)且僅當(dāng)a=b=4時(shí)取得
最新回答 更多>
相關(guān)問答
- 佳能24MM F/2.8和佳能EF-S 10-22mm哪個(gè)更好
- hm 1s刷機(jī)會不會導(dǎo)致硬件出錯(cuò)
- 衛(wèi)星鍋廣電智能卡免費(fèi)的嗎
- owwo1s手機(jī)連不上電腦怎么處理
- 三星手機(jī)740SC怎么解鎖
- 智能助手是什么意思?
- MWNF2CH/A 是什么版本?
- 手機(jī)管家開啟管理里面有一個(gè)智能提醒那個(gè)有用嗎?
- 華為3c升級包那兒下載
- 360手機(jī)衛(wèi)士智能壁紙里頭有張壁紙很好看叫那片海 求圖
- 小米的智能按鈕米鍵有什么用,怎么用
- 為什么手機(jī)撥打10086時(shí),撥通后只有一個(gè)語音提示:智能語音查話費(fèi)查流量請按6,當(dāng)你輸入6后,
- 涂鴉智能的世界地位好不好?
- 索愛k700c突然自動(dòng)關(guān)機(jī),按開機(jī)鍵時(shí)開機(jī)鍵閃紅光是怎么回事啊?是不是沒電了
- htc g10屏幕黑屏,按屏幕還有反映
